The other day I was trying to remember how to construct a simple Oblivious Linear Evaluation (OLE) from Random OLE. I couldn’t find the formula online and it took a few trials to reconstruct it, so I decided to keep it here. There is nothing deep but it’s a good way to recap what OLE is.
Oblivious Linear Evaluation is a two-party protocol. Alice holds an input x from some ring and Bob holds two inputs (a,b). They want to compute ax+b without revealing anything else (i.e. Alice gets ax+b and doesn’t learn anything about a or b, and Bob doesn’t learn anything about x). This picture from Peter Scholl1 summarizes the functionality:
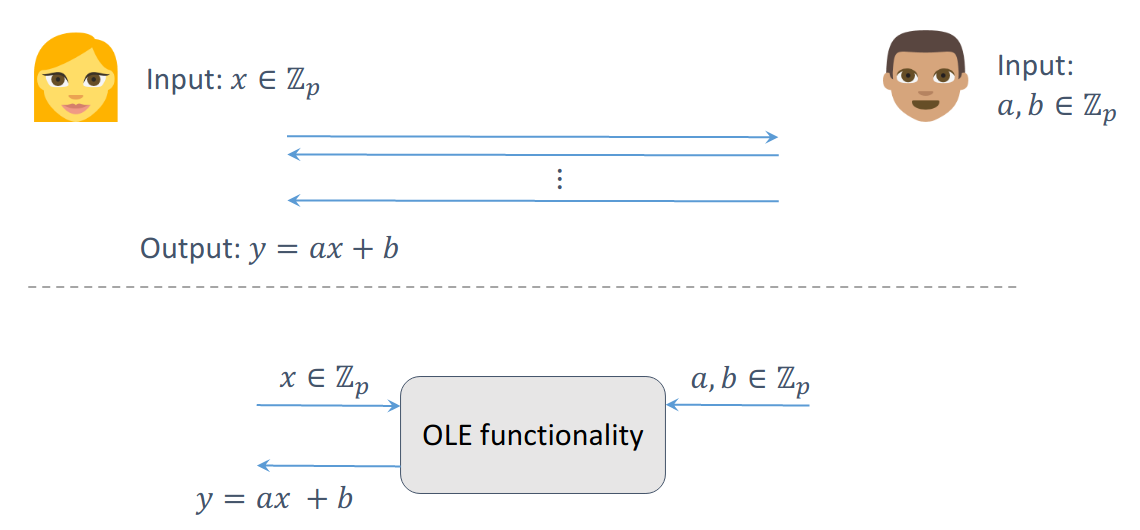
Oblivious Linear Evaluation functionality. Credit: Peter Scholl, 12th BIU Winter School.
Random OLE is a variation of OLE where the inputs x,a,b are random instead of being chosen by the participants.
Then, it is a fact that we can construct (standard) OLE from Random OLE. But how? The idea is to use the outputs of the Random OLE as one-time pads for the true OLE inputs. Here is the explicit protocol:
- Run Random OLE with (random) inputs \(x_r, a_r, b_r\):
$$A: x_r \longrightarrow R-OLE \longleftarrow (a_r, b_r): B$$
$$A: a_r x_r + b_r \longleftarrow R-OLE$$
- Exchange the true inputs \(x,a,b\) – carefully padded with the random values:
$$A: (x - x_r) \longrightarrow B $$
$$A \longleftarrow a_r(x-x_r) + b - b_r : B$$
$$A \longleftarrow (a - a_r): B$$
- Finally, Alice can reconstruct the desired output:
$$(a_r x_r + b_r) + a_r(x-x_r) + b - b_r + (a - a_r)x = a_r x + (a - a_r)x + b = ax + b$$
We can verify that in the honest-but-curious case Alice and Bob don’t learn each other’s inputs.
Source: 12th BIU Winter School ↩︎